GisSOM-ohjelmisto monimuuttuja-aineiston klusterointiin – Itseorganisoituvat kartat

Itseorganisoituvat kartat

Kuten ensimmäisessä blogissa kerrottiin, itseorganisoituva kartta (SOM, self-organizing map) on hila, jolle samankaltaiset mittauspisteet järjestäytyvät lähelle toisiaan. Tällainen esitystapa avaa uusia mahdollisuuksia prosessoida ja tulkita aineistoa. SOM:n käyttöä saattaa rajoittaa laskentakapasiteetti, mikäli mittauspisteiden tai muuttujien määrä on hyvin suuri. Tulosten hyödyllisyyttä ajatellen mittauspisteitä tulisi kuitenkin olla mahdollisimman paljon. Geotieteellisessä aineistossa muuttujien määrä voi olla luokkaa kymmenen, kun käsitellään geokemiallista tai -fysikaalista aineistoa, ja luokkaa sata tai jopa tuhat, kun kyseessä ovat spektriaineistot. Mittauspisteiden määrä vaihtelee tavallisesti kymmenistä miljooniin.

Muuttujien ja mittauspisteiden määrä vaikuttaa tapaan, jolla SOM tulosta tulkitaan. Vertaamme tässä kahdelle aineistolle tehtyä SOM analyysiä. Ensimmäinen aineisto koostuu mineraalinäytteiden spektrimittauksista; tässä tapauksessa yhdestätoista mittauspisteestä (mineraalinäytteet), joille on mitattu yli 150 muuttujan arvot (spektrikanavilla mitatut intensiteetit). Toinen aineisto on satelliittikuva, johon tutustuttiin blogisarjan edellisessä kirjoituksessa. Kuvassa on noin 650 000 mittauspistettä (pikseliä) ja kolme muuttujaa (R, G ja B värit).

Ennen kuin käydään läpi miten SOM:a käytetään esimerkkiaineistojen luokitteluun, kokeillaan miten SOM:n voi muodostaa ilman tietokonetta.

Manuaalisesti tehty SOM

Kuten jo nimi “itseorganisoituva kartta” kertoo, SOM on kartta eli pistehila. Kuvitellaan, että olemme keränneet ämpärillisen eri kokoisia, muotoisia ja värisiä taikakiviä. Tarkkaan ottaen kiviä on 10 000. Tehtävänä on antaa yleiskuva siitä, minkä värisiä, muotoisia ja kokoisia kiviä ämpärissä on. Yksi vaihtoehto on tyhjentää nuo 10 000 kiveä maahan ja tuijottaa niitä kotvanen yrittäen ymmärtää millaisia ne ovat. Tämä ei kuitenkaan johtaisi kovin hyvään lopputulokseen, joten teemme työn hieman järjestelmällisemmin. Piirrämme maahan ristikkohilan, sanotaan 10 x 10 ruutua, ja asetamme jokaiseen ruutuun yhden kiven ämpäristä. Hilassa on lopulta 100 kiveä, mutta ne ovat täysin satunnaisessa järjestyksessä ajatellen niiden muotoa, väriä ja kokoa. Edelleen on hankala nähdä millaisia erilaisia ominaisuuksia kivijoukko edustaa. Lisäksi nuo 100 kiveä ovat liian pieni osajoukko edustaakseen koko 10 000 kiven populaatiota. Jos pystyisimme järjestämään kivet hilaan siten, että samanlaiset kivet ovat lähellä toisiaan ja jos voisimme lisäksi varmistaa, että hilan 100 kiveä edustavat ominaisuuksiltaan koko populaatiota, pystyisimme helposti saamaan käsityksen kivien ominaisuuksista ämpärissä.

Tämä on mahdollista, kun teemme niin kuin Kohonen on opettanut (Kohonen T., 2001, Self-organizing maps, Springer) ‒ ja koska kivemme ovat taikakiviä. Otamme yhden kiven ämpäristä ja etsimme hilalla jo olevista kivistä sen, joka on ominaisuuksiltaan lähinnä ämpäristä otettua. Kutsukaamme tätä hilan kiveä termillä ”paras osuma” (BMU, best matching unit). Kun nyt tuomme ämpäristä otetun kiven BMU:n lähelle, muuntuu BMU ominaisuuksiltaan hieman lähemmäs ämpäristä otettua kiveä. Myös BMU:n lähellä olevat kivet muuntuvat, mutta sitä vähemmän mitä kauempana BMU:sta ne ovat. Kun hilan kivien ominaisuudet ovat muuntuneet hieman lähemmäs ämpäristä otetun kiven ominaisuuksia, laitetaan ämpäristä otettu kivi syrjään, esimerkiksi toiseen ämpäriin. Seuraavaksi otamme toisen kiven ensimmäisestä ämpäristä, etsimme hilalta sitä lähinnä olevan BMU:n ja muunnamme jälleen BMU:n ja sitä lähellä olevien hilan kivien ominaisuuksia. Näin toimii SOM. Kun olemme käyneet läpi ämpärillisen kiviä kyllin monta kertaa, edustavat hilalla olevat muuntuneet kivet ämpärissä olevan 10 000 kiven ominaisuuksia ja vieläpä niin, että samankaltaiset kivet ovat hilalla lähellä toisiaan.

Tässä esimerkissä käytimme näköaistia vertaillessamme kivien ominaisuuksia. Jos haluamme säästää aikaa ja muodostaa SOM:n käyttämällä tietokonetta, meidän tulee määrittää kivien ominaisuuksia kuvaavat parametrit, jotka voi antaa muuttujina laskentaohjelmalle. 7‒10 parametria riittää kuvaamaan kiven muotoa, kokoa ja väriä. Määrittääkseen kahden kiven ominaisuuksien eron, ohjelma laskee eron annettujen parametrien arvojen välillä. Muuntaakseen hilalla olevan kiven ominaisuuksia, ohjelma käyttää muuntuvan ja muuntavan kiven parametrien arvoja sekä yksinkertaisia laskentakaavoja. Ämpärissä olevien kivien ominaisuudet annetaan ohjelmalle numeerisena taulukkona, jossa esimerkiksi kullakin rivillä on omissa sarakkeissaan yhden kiven ominaisuusparametrien arvot. SOM-ohjelma lukee yhden rivin (kivi) kerrallaan, vertaa sillä olevia parametrien arvoja hilalla olevien jo muuntuneiden kivien parametrien arvoihin, määrittää BMU:n ja muuntaa sitä ja sen naapureiden parametrien arvoja. Aivan ensimmäisten kivien valinnan hilalle voi tehdä monella tavoin. Se voi olla satunnaisotos kivistä ämpärissä tai laskentaohjelmaa käyttämällä mikä tahansa otos parametrien arvoja, joka jollain tavoin edustaa kiviämpärillisen ominaisuuksia.

Mineraalinäytteiden spektriaineiston SOM

Nyt kun on selvää miten SOM muodostuu, sitä voidaan soveltaa oikeaan mittausaineistoon. NEXT-projektissa Yong-Hwi Kim Lorrainen yliopistosta käytti GisSOM:a analysoidakseen mineraalien spektriaineistoa. Mittausaineistona toimi taulukko mitattujen näytteiden spektreistä, jossa kullakin rivillä oli yksi näyte ja kussakin sarakkeessa mitattu spektrisuure (Taulukko 1). Ajatuksena oli tutkia miten eri mineraaleja edustavat näytteet sijoittuvat SOM:lle, ja auttaako SOM erottamaan spektrien perusteella eri mineraalit toisistaan.

Taulukko 1. Esimerkki spektriaineistosta, jossa Ns näytteelle on mitattu intensiteetti Nwl aallonpituudella.

Näyte	Aallonpituus 1	Aallonpituus 2	…	Aallonpituus Nwl
Näyte 1	0.2	0.2	…	0.58
Näyte 2	0.24	0.3	…	0.65
…	…	…	…	…
Näyte Ns	0.1	0.3	…	0.7

Mittaukset suoritettiin yhdelletoista näytteelle, jotka edustivat kuutta eri karbonaattimineraalia. Aineistossa oli yhteensä yli 150 muuttujaa mitattuna neljällä spektroskopisella menetelmällä. Näin suuri määrä muuttujia vaatii laskennallisten menetelmien käyttöä. Tosin geologi saattaisi sanoa: ”Ajan haaskausta! Olisin tunnistanut mineraalit alkuperäisistä kivinäytteistä hetkessä”. Mutta se on toinen tarina.

Koska laskennallisten menetelmien käytön hyöty tässä tapauksessa vaikutti ilmeiseltä, suoritettiin SOM laskenta GisSOM-ohjelmistolla. Verrattuna kiviesimerkkiin, mineraaliaineistossa oli hyvin vähän mittauspisteitä (11 vs 10 000) ja huomattavasti enemmän muuttujia (150 vs 7‒10). Tämä ei sinällään vaikuta SOM laskentaan, mutta siihen kylläkin miten tuloksia tulkitaan. Mineraaliaineiston tapauksessa emme ole niinkään kiinnostuneita muuttujien arvojen jakaumasta SOM:lla, vaan 11 mittauspisteen sijoittumisesta SOM hilaan. Kivien tapauksessa tilanne oli päinvastainen.

Kun GisSOM laskenta käynnistettiin, löysivät mineraalinäytteet nopeasti paikkansa 10×10 kokoisessa SOM hilassa, ja niiden vaikutus levittäytyi myös kutakin mittauspistettä vastaavan BMU:n ympäristöön ‒ vähän kuin tiputettaessa erivärisiä pisaroita märälle akvarellipaperille. Vaikka vain pieni osa SOM hilan pisteistä toimi BMU:na mineraalinäytteille (11 näytettä vs 100 hilapistettä), oppivat muutkin pisteet SOM laskennan aikana ja laskennan valmistuttua kaikkien hilapisteiden voitiin ajatella edustavan näytteiden spektriarvoja. Jotta nähtiin mitä mineraalia kukin hilapiste edustaa, klusteroitiin SOM käyttämällä k-means algoritmia ja hilapisteet väritettiin klusterin mukaisesti (Kuva 1).

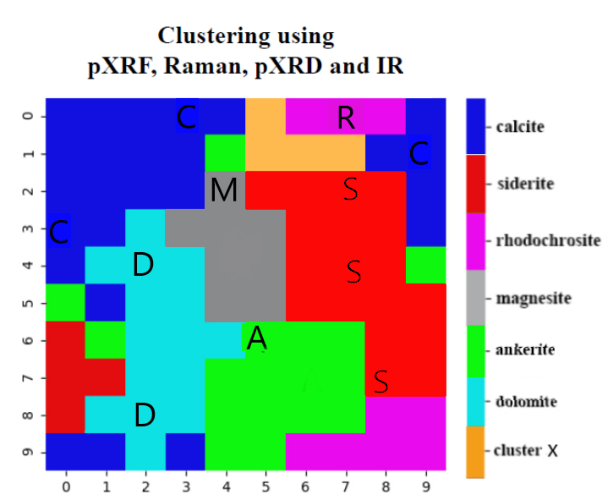
Kuten edellisessä blogissa mainittiin, klusterilla ei ole ennalta määrättyä roolia tai merkitystä. Mineraaliaineiston tapauksessa kaikkien näytteiden todellinen luokka (mineraali) tunnettiin, mutta tätä tietoa ei käytetty SOM tai k-means laskennoissa. Klusterit voitiin kuitenkin muuntaa yksikäsitteisesti luokiksi, koska samaan klusteriin sijoittuvat BMU:t (hilapisteet, joita vastaa mittauspiste) edustivat vain yhtä mineraalia. Mineraalispektriaineisto on hyvä esimerkki siitä, miten SOM:a voi käyttää ennustamaan spektrejä, joita aineistossa ei esiinny. Voidaan nimittäin olettaa, että kaikki SOM hilapisteet, jotka kuuulvat samaan luokkaan, edustavat samaa mineraalia tai kenties klustereiden rajalla kahden mineraalin seosta. Esimerkiksi koko punainen alue Kuvassa 1 edustaa mahdollisia sideriittinäytteiden spektrejä tai mahdollisesti alueen reunoilla mineraaliseosten spektrejä.

Mineraalispektrien ja satelliittikuvan SOM tulkintojen ero

Koska ensimmäisessä blogissa käsiteltiin tarkemmin satelliittikuvan SOM tuloksia, keskitytään tässä vertaamaan niitä ja mineraalispektreille lasketun SOM laskennan tuloksia. Merkille pantavaa on jo lähtöaineistojen erilaisuus. Satelliittiaineistossa on vain kolme muuttujaa, kun mineraalispektriaineistossa niitä on yli 150. Mittauspisteitä satelliittiaineistossa on puolestaan huomattava määrä (n. 650 000 pikseliä) verrattuna mineraalinäytteisiin (11 kpl). Mineraalinäytteille lasketun SOM hilan koko oli noin kymmenkertainen näytemäärään nähden, kun taas satelliittikuvan SOM:ssa jokainen hilapiste itsessään on jo vähintään kymmenien mittauspisteiden klusteri.

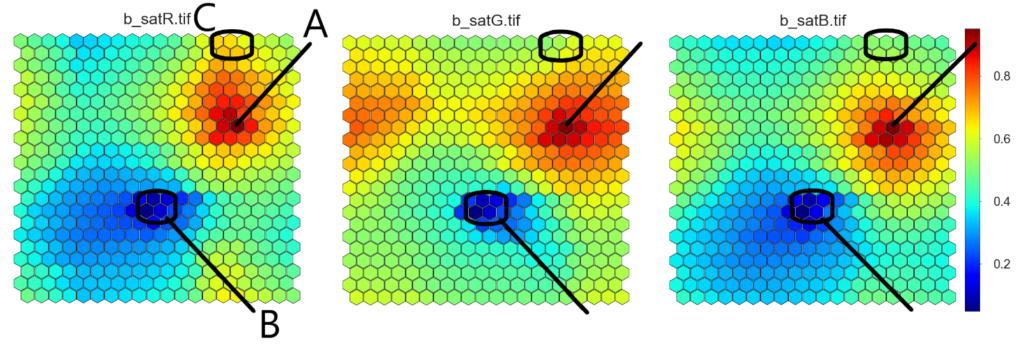
Mineraalispektrien SOM:n muuttujakohtainen visualisointi kannattaa vain, jos hyvin rajallinen määrä spektriarvoja riittää erottamaan mineraaleja toisistaan. Satelliittikuvan kaikki kolme muuttujaa sen sijaan on helppo visualisoida SOM hilassa (Kuva 2). Kuten edellisessä blogissa kerrottiin, näkee muuttujakohtaisista SOM kuvista, että satelliittikuvan yleissävy on vihreä, mutta siinä on tummia (B) ja valkoisia (A) alueita, sekä alueita, joissa punainen sävy hallitsee (C).

Satelliittikuvan SOM hila klusteroitiin k-means algoritmia käyttämällä (Kuva 3). Klustereita ei tässä tapauksessa käytetä määrittämään havaitsemattomia muuttujien arvoja kuten mineraalispektriaineiston tapauksessa tehtiin, koska mittauspisteitä on jo niin paljon, että niistä voidaan suoraan määrittää arvojakaumat. Satelliittikuva-aineiston klusterit ovat sen sijaan hyödyllisiä ryhmittelemään mittauspisteitä ja rajaamaan homogeenisia alueita tutkimusalueella.

SOM menetelmän ydin on SOM hila, johon aineisto järjestyy. SOM antaa yleiskuvan aineistosta ja auttaa ymmärtämään sen rakennetta sekä löytämään mahdollisesti toisistaan erottuvia populaatioita. SOM tuloksen voi visualisoida monella tavalla muuttujakohtaisten SOM hilojen ja klusteroinnilla erotettujen osa-alueiden lisäksi. Esimerkiksi vierekkäisten hilapisteiden ero näyttää klustereiden rajapinnat ja kuhunkin hilapisteeseen osuneiden mittauspisteiden lukumäärä liittyy alkuperäisen aineiston jakaumaan.

Kohti GisSOM-ohjelmiston esittelyä

Nyt olemme kuvanneet miten SOM toimii ja esitelleet sen soveltamista kolmeen erilaiseen aineistoon. Pohdimme mittauspisteiden, muuttujien määrän ja SOM hilan koon vaikutusta tulosten tulkintaan. Miten sitten SOM laskenta tehdään käytännössä? Tähän kysymykseen vastataan seuraavassa, sarjan viimeisessä blogissa GisSOM-ohjelmisto monimuuttuja-aineiston klusterointiin – GisSOM, jossa viimein päästään esittelemään GisSOM-ohjelmistoa.

Blogisarjan ensimmäinen osa: GisSOM-ohjelmisto monimuuttuja-aineiston klusterointiin ‒ Katsaus klusterointiin ja itseorganisoituviin karttoihin

Mikäli haluat vilkaista GisSOM-ohjelmistoa, löydät sen GitHubista, josta sen voi ladata ja asentaa.

GisSOM-ohjelmisto on kehitetty Euroopan Unionin Horisontti 2020 ohjelmasta rahoitetussa NEXT projektissa (Grant Agreement No. 776804 – H2020-SC5-2017 NEXT – New Exploration Technologies).

Teksti:

Johanna Torppa, erikoistutkija, Tietoratkaisut, johanna.torppa@gtk.fi

Viitteet:

Kohonen, T. 2001. Self-organizing maps. Springer.